La circunferencia goniomética, trigonométrica, unitaria o unidad es una circunferencia de radio unitario, normalmente con su centro en el origen (0, 0) de un sistema de coordenadas cartesianas, de un plano euclídeo.
Dicha circunferencia se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas, mediante la representación de triángulos rectángulos auxiliares.
Si (x, y) es un punto de la circunferencia unidad del primer cuadrante, entonces x e y son las longitudes de los catetos de un triángulo rectángulo cuya hipotenusa tiene longitud 1. Aplicando el teorema de Pitágoras, x e y satisfacen la ecuación:
La circunferencia goniomética, trigonométrica, unitaria o unidad es una circunferencia de radio unitario, normalmente con su centro en el origen (0, 0) de un sistema de coordenadas cartesianas, de un plano euclídeo.
Dicha circunferencia se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas, mediante la representación de triángulos rectángulos auxiliares.
Si (x, y) es un punto de la circunferencia unidad del primer cuadrante, entonces x e y son las longitudes de los catetos de un triángulo rectángulo cuya hipotenusa tiene longitud 1. Aplicando el teorema de Pitágoras, x e y satisfacen la ecuación.
Marta & Jose
miércoles, 4 de mayo de 2011
jueves, 9 de diciembre de 2010
jueves, 2 de diciembre de 2010
miércoles, 3 de noviembre de 2010
Polinomios
Polinomios
Un polinomio es una suma de términos llamados monomios.Un monomio es el producto de un coeficiente (un número real), una variable (casi siempre x o y) elevada a un exponente (entero positivo). Existen polinomios con uno, dos o más términos, por ejemplo:
- Monomio (un término): 5 x2 En este caso el coeficiente es 5, la variable es x el exponente 2
- Binomio (dos términos): 6 x7 - 2
- Trinomio (tres términos): 3 x5 + 4 x3 - x2
En este trabajo utilizaremos polinomios con coeficientes enteros y potencias enteras positivas.
Grado de un polinomio
El grado de un polinomio es igual al exponente mayor de la variable. Por ejemplo:| 5 x2 | Es un polinomio de grado 2 |
| 6 x7 - 2 | Es de grado 7 |
| 3 x5 + 4 x3 - x2 | Es de grado 5 |
| 2 x4- x3 - x2 | ¿De qué grado es? |
| 6 x5 - 4 x2 - 19 x | ¿De qué grado es? |
| 3 x15 + x13 - x2 | ¿De qué grado es? |
| 13 | ¿De qué grado es? |
Nota cómo se deben escribir los polinomios. Se deben escribir en orden decreciente con respecto al grado de cada término.
Raíces de un polinomio
La raíz de un polinomio es un número tal que hace que el polinomio valga cero. Es decir que, cuando resolvamos un polimonio a cero, las soluciones son las raíces del polinomio. Por ejemplo el polinomio| f(x) = x2 + x - 12 |
| x2 + x - 12 = 0 | Igualando a cero. |
| (x + 4)(x - 3) = 0 | Factorizando. |
| x = - 4 | Solución 1 |
| x = 3 | Solución 2 |
Puesto que x1 = - 4 y x2 = 3 son soluciones de f(x) entonces f( -4 )= 0 y f( 3 )= 0. Decimos entonces que x = - 4 y x = 3 son raíces del polinomio f(x)= x2 + x - 12
Las raíces de f(x) = x3 - 4 x2 + x + 6 son x = - 1, x = 2 y x = 3 ¿Por qué?
Factorización de un polinomio
El número de factores en que se puede descomponer un polinomio es igual al grado del polinomio (Teorema fundamental del Álgebra).Para que podamos factorizar un polinomio es necesario encontrar sus raíces. Cuando ya lasntengamos, los factores correspondientes a cada raíz son de la forma ( x - r ) donde r es una de las raíces. Esto es, si r1, r2, ... , rn son raíces del polinomio f(x) entonces la factorización de f(x) es:
Por ejemplo, si
f(x) = x3 - 4 x2 + x + 6 como sus raíces son x = - 1, x = 2 y x = 3 entonces f(x) se ha factorizado como
f(x) = (x - (-1)) (x - 2) (x - 3) = (x + 1) (x - 2) (x - 3)
f(x)= x2 + x - 12 como sus raíces son x = - 4 y x = 3 entonces f(x) se ha factorizado como
f(x) = (x - (-4)) (x - 3) = (x + 4) (x - 3)
Representación gráfica de las raíces de un polinomio
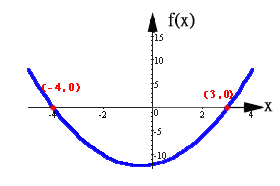
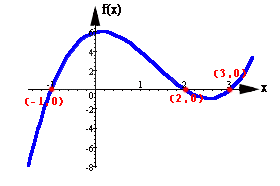
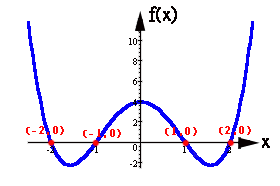
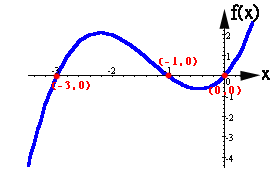
Como las raíces de un polinomio hacen que éste valga cero, en un plano cartesiano esto lo identificamos como las intersecciones de la gráfica del polinomio con el eje de las X (abscisas).Esto es, los puntos en donde cruza la gráfica al eje horizontal tienen como abscisa la raíz del polinomio graficado. A continuación presentamos algunas funciones con sus raíces, factores y gráficas:
Teorema fundamental del Álgebra
Carl Friedrch Gauss ha sido uno de los matemáticos más grandes de todos los tiempos. Contribuyó a muchas ramas de las matemáticas. En 1798, ¡ a los 20 años de edad !, Gauss demostró el teorema fundamental del Álgebra que dice lo siguiente:Una forma en la que podemos interpretar este teorema es como sigue, ya que se puede factorizar un polinomio dadas las raíces y hay n raíces para todo polinomio de este grado, entonces:
donde r1, r2, ... , rn son las raíces de f(x).
La demostración de este teorema queda lejos del objetivo de esta página sin embargo daremos algunas herramientas para encontrar las n raíces.
Regla de los signos de Descartes
Rene Descartes (el mismo del plano cartesiano) encontró un método para indicar el número de raíces positivas en un polinomio. Esta regla dice lo siguiente:Por ejemplo el polinomiof(x)= x2 + x - 12 tiene un cambio de signo, del segundo al tercer término, por lo tanto tiene una raíz positiva.
g(x)= +x3 - 4 x2 + x + 6 tiene dos cambios de signo, tiene dos raíces positivas
h(x)= +x4 - 5 x2 + 4 tiene dos raíces positivas
i(x)= x3 + 4 x2 + 3 x No tiene cambios de signo, por lo tanto no tiene raíces reales positivas.
j(x)= x3 - 2 x2 - 5 x + 6 ¿Cuántas raíces positivas tiene?
Conjunto de posibles raíces
Existe un método para encontrar un conjunto de números, los cuales pueden ser raíces de un polinomio. La regla que mencionarémos aquí es aplicable sólo para polinomios con el coeficiente de la potencia mayor de x igual a 1. Es decir, si f(x) = an xn + an-1 xn-1 + an-2 xn-2 + an-3 xn-3 + ... + a3 x3 + a2 x2 + a1 x + a0 tomarémos a an = 1. Esto es que sólo trabajarémos con polinomios de la siguiente forma:f(x) = xn + an-1 xn-1 + an-2 xn-2 + an-3 xn-3 + ... + a3 x3 + a2 x2 + a1 x + a0
El conjunto de posibles raíces de f(x) se forma con los divisores de a0 (del término independiente), hay que considerar estos divisores tanto con signo positivo como con negativo. La forma en que podemos usar esta información del término independiente es la siguiente, puesto que cualquier elemento de este conjunto puede ser raíz de f(x) hay que evaluar a f(x) en algun valor de este conjunto y si el resultado de la evaluación es cero, entonces ese valor escogido es raíz de f(x). En la siguiente tabla mostramos varios polinomios, los divisores del término independiente y las raíces de los polinomios:
| Función | Divisores del término independiente | Raíces |
| f(x)= x2 + x - 12 | 1, 2, 3, 4, 6, 12, -1, -2, -3, -4, -6, -12 | - 4 y 3 |
| f(x)= x3 - 4 x2 + x + 6 | 1, 2, 3, 6, -1, -2, -3, -6 | - 1, 2 y 3 |
| f(x)= x4 - 5 x2 + 4 | 1, 2, 4, -1, -2, -4 | - 2, - 1, 1 y 2 |
| f(x)= x3 - 2 x2 - 5 x + 6 | 1, 2, 3, 6, -1, -2, -3, -6 | 1, - 2 y 3 |
¿Qué hacer cuando tengamos una raíz?
Con lo visto en los apartados anteriores tenemos las herramientas necesarias para encontrar las n raíces de un polinomio. Recordemos que para encontrar una raíz es necesario saber los divisores del término independiente y evaluar nuestro polinomio en con el valor escogido. Además de haber encontrado una raíz usando el método anterior hemos hallado un factor de nuestro polinomio. Podemos estar seguros de que si r es una raíz de f(x) entonces al dividir f(x) / (x - r) tendrémos como resultado un polinomio de un grado menor a f(x) y como residuo cero.Así hemos reducido nuestro prolema de encontrar n raíces en otro peroblema, el encontrar sólo n-1 raíces.
jueves, 21 de octubre de 2010
miércoles, 13 de octubre de 2010
Trabajo de nº reales
Nº REALES
En matemáticas, los números reales son aquellos que poseen una expresión decimal e incluyen tanto a los números racionales como a los números irracionales.
Los números reales no se utilizaron en Europa hasta el siglo XVII. En ese siglo, en el cálculo se utilizaba un conjunto de números reales sin una definición concisa, cosa que finalmente sucedió con la definición rigurosa hecha por Georg Cantor en 1871.
En realidad, el estudio riguroso de la construcción total de los números reales fue lograda en el siglo XIX por dos grandes matemáticos europeos utilizando vías distintas: la teoría de conjuntos de Georg Cantor, por un lado, y el análisis matemático de Richard Dedekind .Ambos matemáticos lograron la sistematización de los números reales en la historia, no de manera espontánea, sino utilizando todos los avances previos en la materia.
 Números Naturales. Dicho en términos muy simples, los números naturales son los que sirven para contar.
Números Naturales. Dicho en términos muy simples, los números naturales son los que sirven para contar.Números Enteros. El conjunto de números enteros, es infinito. Son parejas de números naturales (x,y), cuya resta x-y define un número entero. Existe un isomorfismo entre parte del conjunto de los números enteros y el de los números naturales; ya que el conjunto de los naturales esta en el de los enteros positivos.
Números Racionales. El conjunto de números racionales está integrado por parejas de números enteros cuyos elementos se dividen entre sí. Los racionales serán positivos o negativos según sea el signo de cada uno de los integrantes de las parejas que los definen. Así será que parejas de enteros de igual signo definirán un racional positivo; y parejas de enteros de distinto signo definirán un racional negativo.
Números Reales. El campo de los números reales es más amplio que el de los racionales; ya que incluye números que no están formados por parejas de enteros. Por ejemplo la relación que existe entre una circunferencia y su diámetro, no es un racional. Se trata de un conjunto infinito. Siempre entre dos números reales hay otro número real; de ahí que se asocie al conjunto de los números reales con una recta. La recta está formada por infinitos puntos y cada punto representaría un número real.
Suscribirse a:
Comentarios (Atom)